Ensemble models
Ensemble models are machine learning models that use more than one predictor to predict. A group of predictors forms an ensemble. In general, ensemble models perform better than using a single predictor. There are three ensemble models, bagging, boosting, and blending.
Random forests
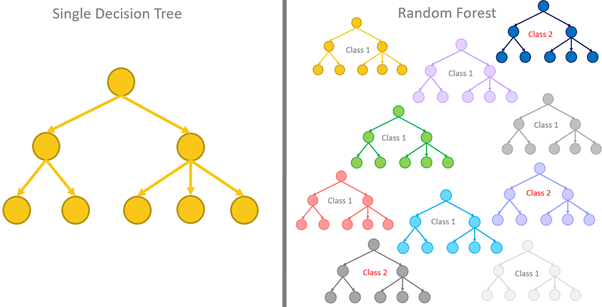
The performance of a single decision tree will be limited, so instead of relying on one tree, a better approach is to aggregate the predictions of multiple trees. On average, the aggregation will perform better than a single predictor. We call a tree-based model that aggregates the predictions of multiple trees a random forest.
There is a need for a diverse collection of trees for a random forest to be effective, so there should be variations in the chosen thresholds for splitting and the number of nodes and branches as there will be no point aggregating the predicted results if all the trees are nearly identical and produce the same result. To achieve a diverse set of trees, we need to: Train each tree in the forest using a different training set and only consider a subset of features when deciding how to split the nodes.
Ideally, we would generate a new training set for each tree for the first point. However, often it’s too difficult or expensive to collect more data; we have to make do with what we have. Bootstrapping is a general statistical technique to generate new data sets with a single set by random sampling with a replacement that allows a data point to be sampled more than once.
Typically, when training the standard decision tree model, the algorithm will consider all features in deciding the node split. Assuming only a subset of your features ensures that your trees do not resemble each other. If the algorithm had considered all features, a dominant feature would be continuously chosen for node splits.
Random forest is also referred to as bagging ensemble models because it is based on bootstrapping and aggregating the results.
The hyperparameters available for random forests include decision trees with some additions.
- n_estimators: The number of trees in the forest.
- n_jobs: The number of jobs to run in parallel when fitting and predicting.
- warm_start: If set to `True,` reuse the trained tree from a prior fitting and just train the additional trees.
Improve the Communication, Integration & Automation of data flow across your Organization
Calculate your DataOps ROI
Extremely Randomized Trees
(ensemble.ExtraTreesClassifier or ensemble.ExtraTreesRegressor)
A variation to the random forest model is an extremely randomized tree that injects additional randomness. A random subset of the features is selected with a random forest to determine which one to use for a node split.
From these randomly chosen values, the best is chosen to perform the split. The extra randomness serves two advantages:
- It helps reduce the model’s variance.
- It leads to faster training times.
Gradient Boosting Trees
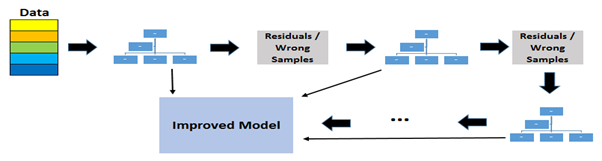
Gradient boosting trees is another ensemble model; it is a collection of tree models arranged in a sequence. Here, the model is built stage-wise; each additional tree will correct the previously built model’s predictions.
Where does the name gradient come from in gradient boosting trees?
Adding a model is analogous to a single iteration in gradient descent. Gradient descent is a minimization algorithm that updates/improves the current answer by taking a step in the direction of the negative gradient of the function minimized. The pseudo-residuals represent the direction of the most significant reduction in prediction error. The learning rate for this model ranges from 0 to 1
The Hyperparameters for this model are:
- Learning_rate: Multiplicative factor of the tree’s contribution to the model.
- Subsample: Fraction of the training data to use when fitting the trees.
Feature importance
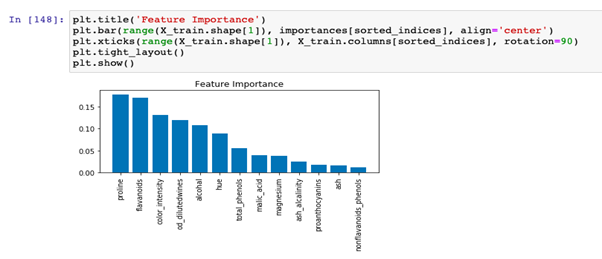
Decision trees can evaluate feature importance. The feature importance score is based on two metrics:
- How many times a particular feature was selected to split a node
- The depth where the feature was chosen to split the node
If a feature is chosen numerous times to make a node split, then it is a feature that is useful in partitioning the training data. The second metric considers the impact of choosing a feature for a node split.
The attribute ‘feature_importance _ provides the feature importance,’ computed as the mean and standard deviation of accumulation of the impurity decrease within each tree.
For example, the feature chosen to perform the initial split of the entire data set will have a greater impact on the tree’s structure than node splits deeper in the tree. For ensemble models, the feature importance is averaged across all trees.








